29. 单位矩阵
单位矩阵
单位矩阵是线性代数中的一种特殊矩阵,在很多应用中都会出现。在本课中,深入了解单位矩阵将有助于理解矩阵求逆。单位矩阵用 \mathbf{I} 符号表示。
\mathbf{I} 是一个n×n方阵,主对角线上的值为 1,其他所有元素都是 0。
对于 1x1 矩阵,单位矩阵如下:
\begin{bmatrix}1\end{bmatrix}
对于 2x2 矩阵,单位矩阵如下:
\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}
对于 3x3 矩阵,单位矩阵如下:
\begin{bmatrix}1 & 0 & 0 \\0 & 1 & 0 \\0 & 0 & 1\end{bmatrix}
对于 4x4 矩阵,单位矩阵如下:
\begin{bmatrix}1 & 0 & 0 & 0 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{bmatrix}
依次类推。
单位矩阵就像数字 1
在标量乘法中,数字 1 有一个特殊的性质:
1\times a = a
。
同样地,
a\times 1 = a
。
单位矩阵具有同样的性质:
\mathbf{AI} = \mathbf{IA} = \mathbf{A}
。虽然单位矩阵总是方阵,但矩
\mathbf{A}
不一定是方阵。
下面是一个乘法的例子:
\mathbf{AI}
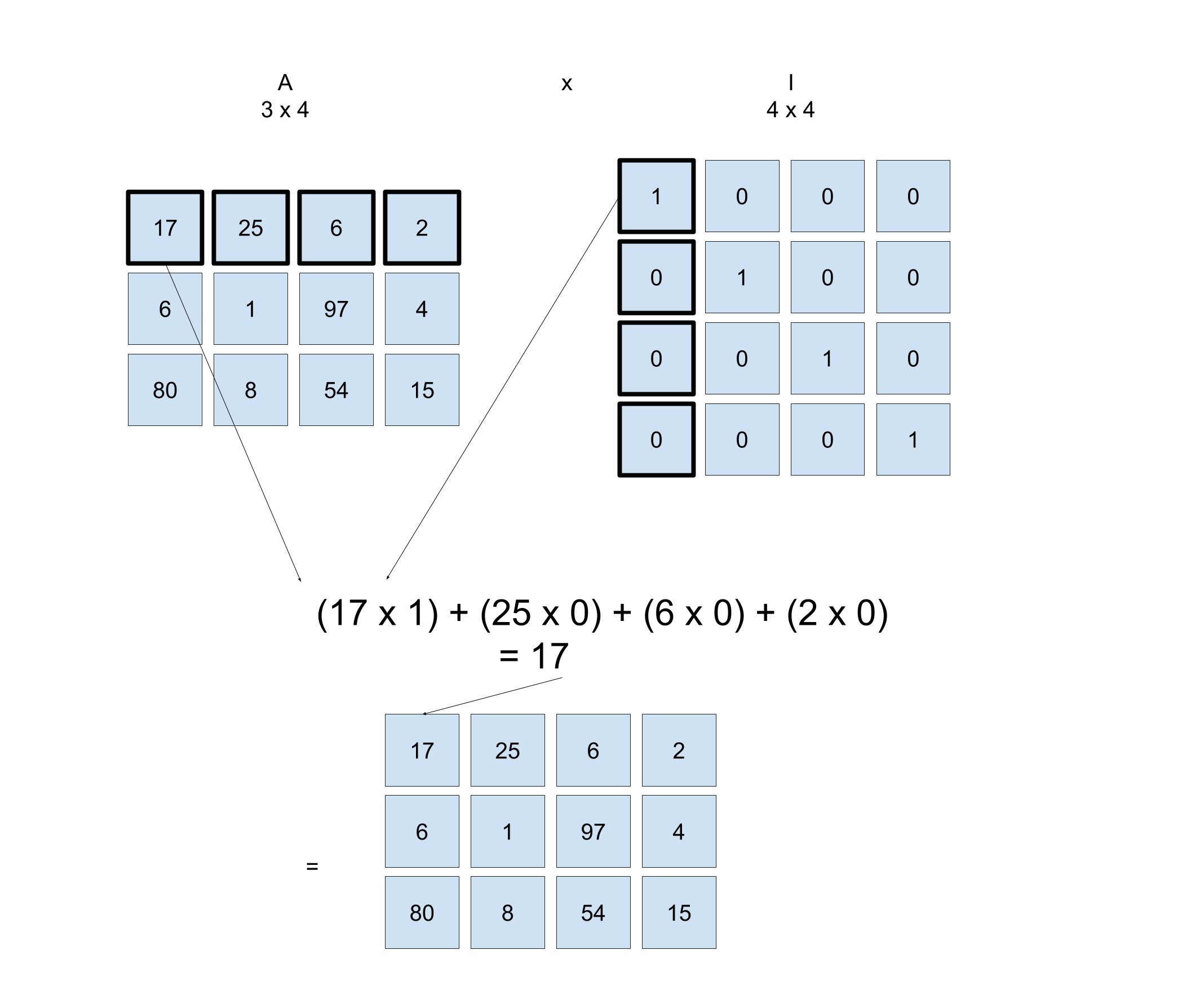
乘以 \mathbf{IA} 的另一种情况呢?你需要考虑 I 和 A 矩阵的维数,才能进行乘法运算。
如何计算 \mathbf{I} 的大小?
输出矩阵必须是 3x4,就像 \mathbf{A} 一样。所以,一个 3×3 的矩阵乘以一个 3×4 的矩阵,会得到一个 3×4 的矩阵。
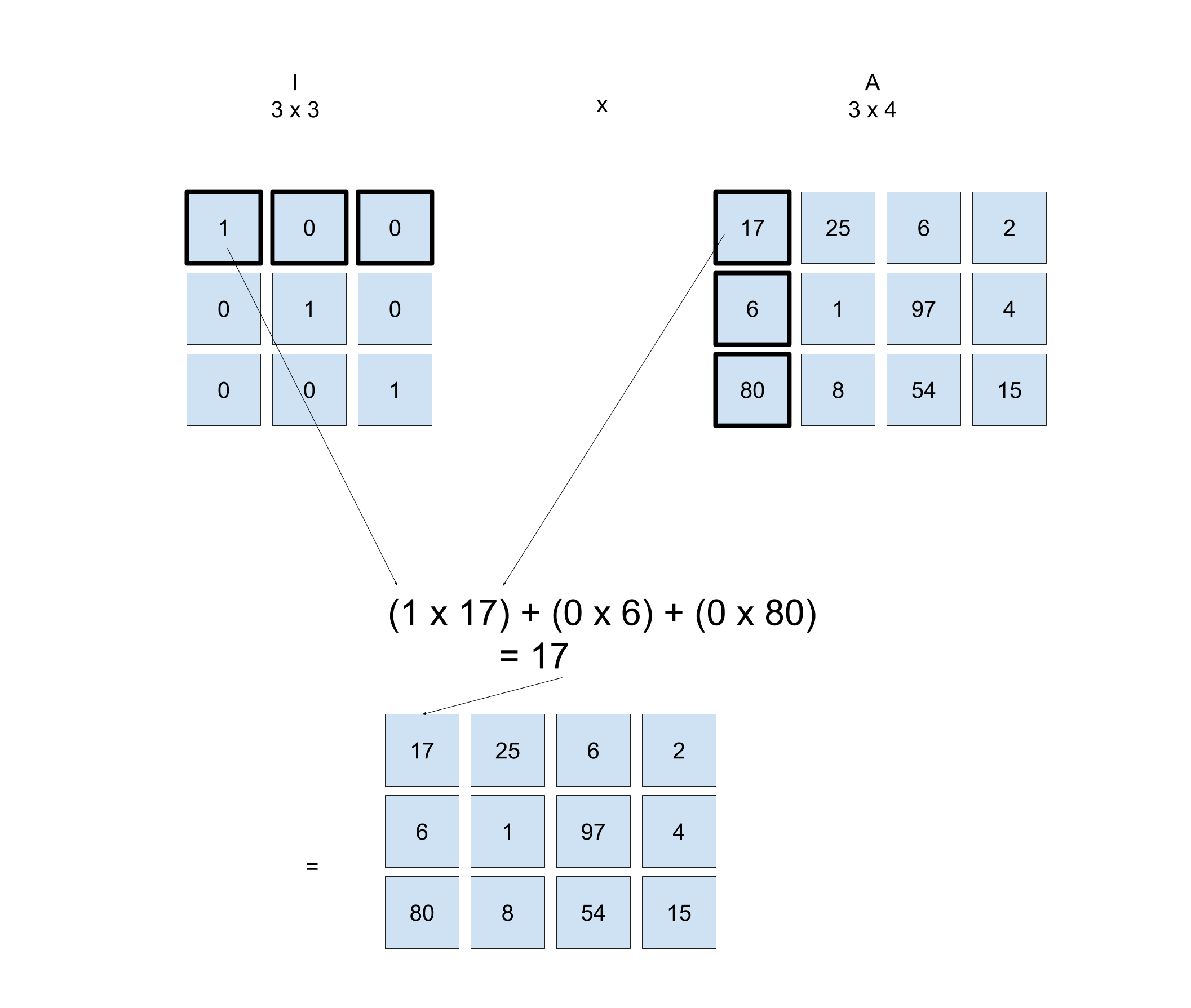
Size of I
SOLUTION:
5x5 与 7x7编程实现单位矩阵初始化
在编程练习中,你需要编写一个函数,该函数会接收一个大小,然后输出该大小的单位矩阵。
考虑一下,如何使用空的 Python 列表开始编程。1 将永远处于指数位置
- [0][0]
- [1][1]
- [2][2]
- [3][3]
- 等等.
矩阵中的其他地方都是 0。所以,你不仅需要使用嵌套 for 循环,还需要使用 if else 语句。